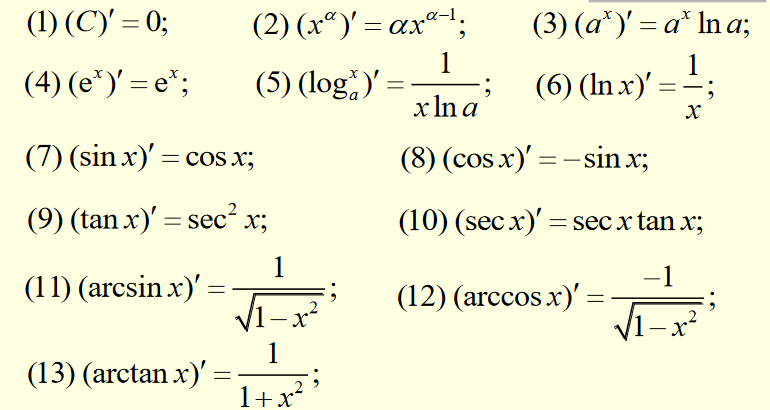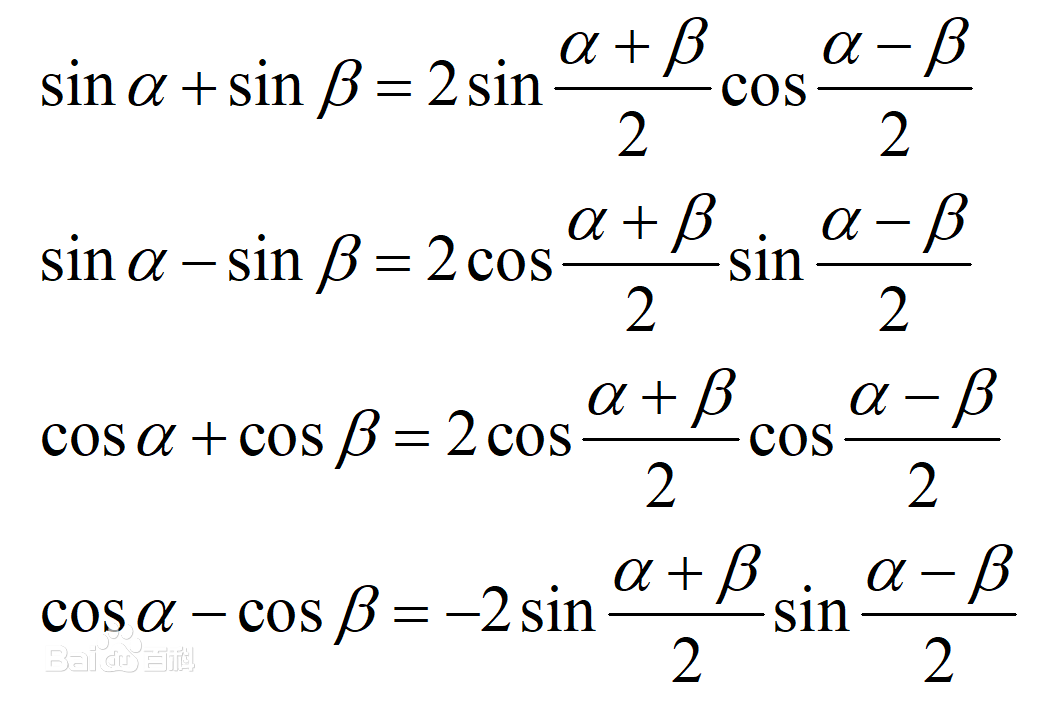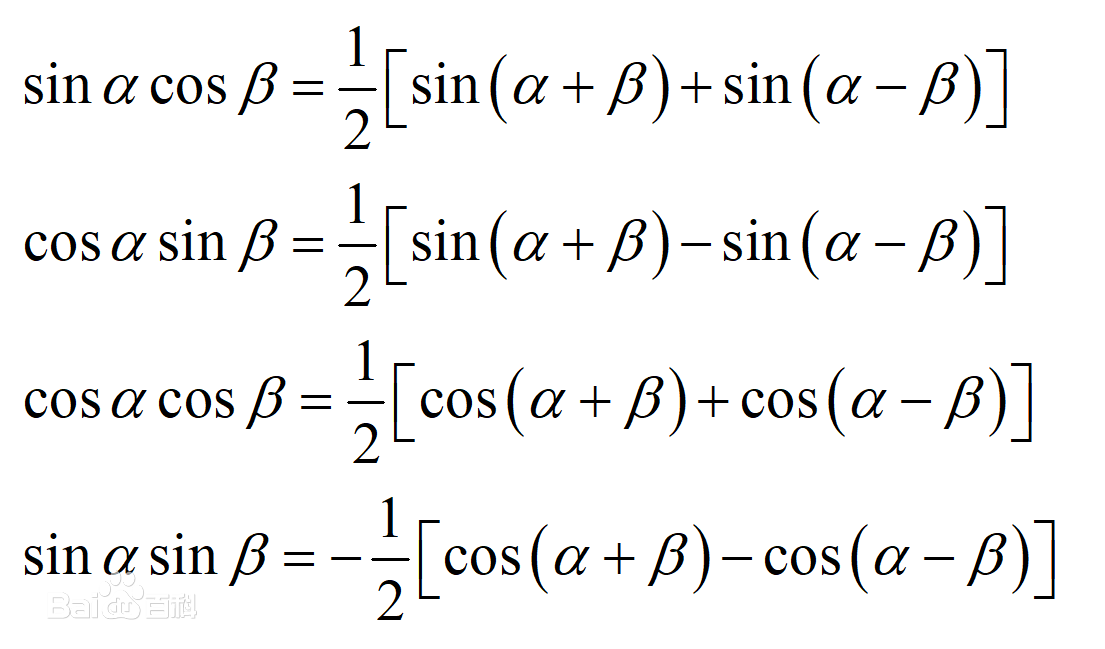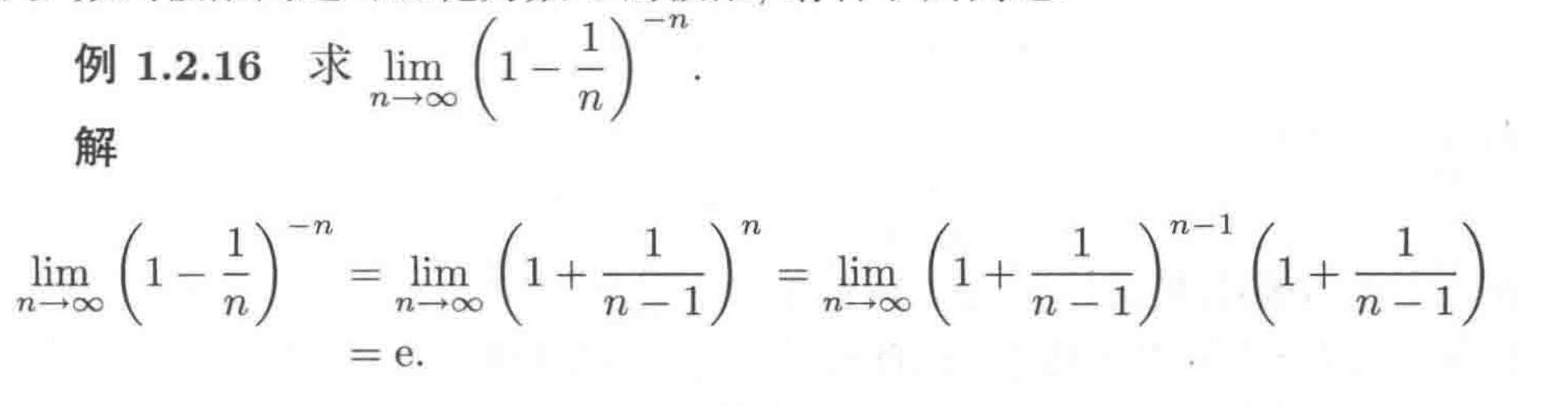写在前面:
- 注意讨论分母是否为0
- 注意讨论极限是否存在
- 适当讨论是否为0可以化简/求出部分
- 极限差为0而商不一定为1(不行,为1(国科大讲义P3)
奇奇怪怪但是很重要的东西
数列重要极限
证明见#二项式定理
函数重要极限
- 连续
- 教材P38 注意左右极限相等
- (其他底数可以使用换底公式)
- (利用 )
- 夹逼定理
(利用)
函数等价无穷小
如:看到
次数高=作用小
基本导数表
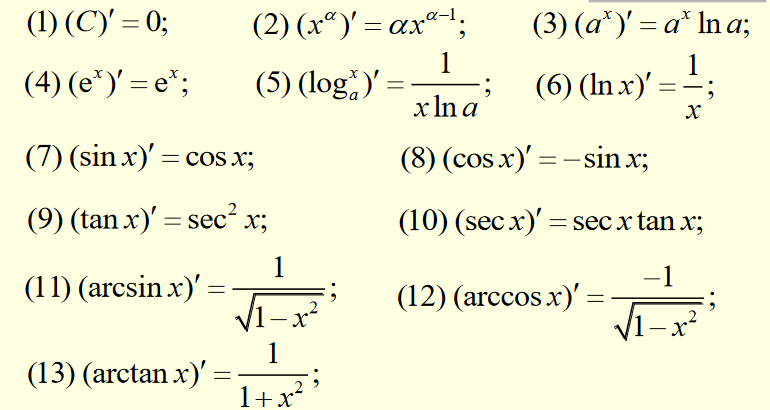
奇奇怪怪的公式
二项式定理

绝对值不等式
当同号推广:
当同号即
两边之差第三边两边之和两边之差小于第三边 + 两边之和大于第三边
伯努利不等式、均值不等式
G:最适用于 不全相同但接近
其中等号当且仅当成立例题4:设证明数列单调递增且
证明:^1e9a3c
解:
由泰勒公式:
整数部分舍弃
奇奇怪怪的证明
极限除法
#epsilon-N定义 + #收敛数列保号性
证明:
使得 #收敛数列保号性
使得
类似地
使得
欲证
#分子拆分
运用 #收敛数列保号性
避免分类讨论
开方
证明:
可以存在运用了 #收敛数列保号性
More about: #次方差展开
证明:
^4e250d
令则且有运用实数公理使有下证①上界不为上界使得②最小
思路: #基本列 中 , 的任意性 + 放缩 + #Cauchy收敛准则

单调数列+发散=>发散到正无穷
例题:证明
证:
自然常数与欧拉常数

- 自然对数的底数,无理数,超越数(非代数数)
超越数(非代数数)的数量远远多于代数数
重要关系
以上命题取对数后等价于:
简证:左边已经证明,右边
- 极限还与数的域有关,有理数域的极限的运算不封闭
- 有理数的数列极限可以构造无理数
- 运用:
-
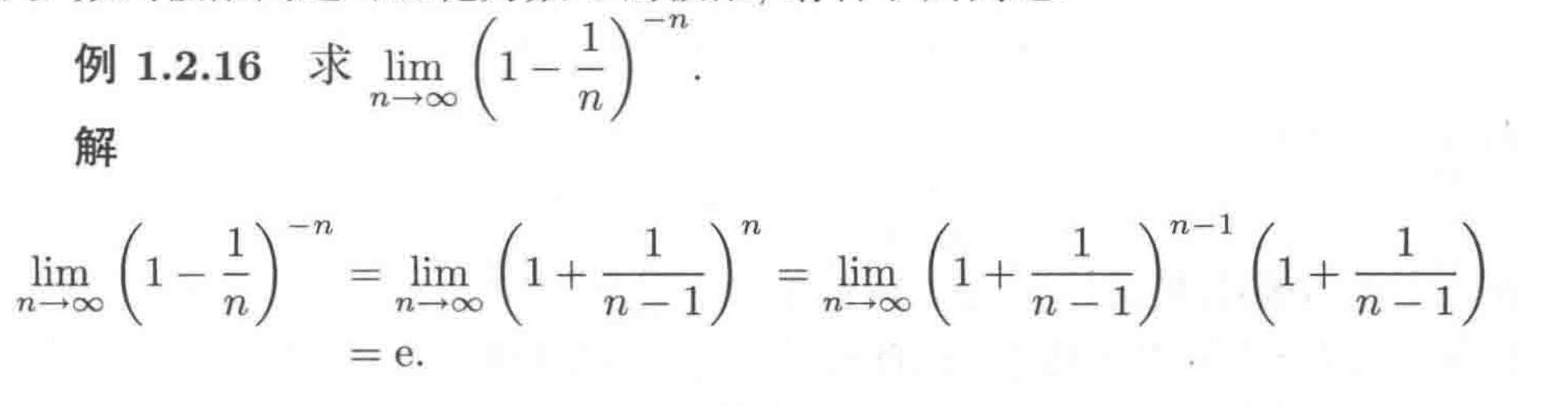
- ※重要 : #欧拉常数
-

证明方程在上有且仅有一根
即:有解
简证:
存在性: #零值定理 1,e
唯一性: 单调!
下略
任何奇次多项式至少有一个实零点
奇奇怪怪的方法
如何证明数列收敛
数列收敛的充分必要条件是是基本列
发散<=>非基本列<=>
如何求解数列极限
简化证明
设数列对常数和满足条件
设
Tips: 只能为绝对常数,如果 含有其他变量,可以通过放缩得到绝对常数
求
- 思路1:奇子列↓有下界,偶子列↑有上界
- 极限不能设为相同的,需要分别设出再证明相等
- 思路2:简化+放缩
直接法
适当放大法
#适当放大法 用于:不能解、解很复杂
- 设小于1的某个复杂常数
Eg.
- 合并、拆分=>凑出能约分的常见极限
Eg.
证:需要此时去掉也可以乘再趋于
此时应该取,下略
- 不等式、二项式等公式
Eg.

- 放缩==(抓大放小)== + #收敛数列夹逼性
Eg.
形定理
设是两个数列且严格递增趋于如果
则有
其中可以是 实数(有界数) / / 只能是定号无穷
Cauchy定理
算数平均
逆命题不成立:极限不存在
证明: 即可
几何平均
连乘
见下
如何证明函数极限存在
函数在时有极限的充要条件是
对于任意一个以为极限的数列都有\lim\limits_{n\to x_{0}}f(a_{n})=l$
设在内单调有界则存在, 不能得出存在
证明只需要在, 运用 #单调函数极限定理 即可
存在
其他五种极限不再赘述
如何求解函数极限
见下
幂指函数
幂指函数极限
- #e的转化
简证:第二个等号运用了 #变量代换 :
- #幂指同时取极限
设则
简证:
- #1∞形不定式
设则
简证:
运用 #幂指同时取极限 :
#e的转化
解:
法一:
#LHospital法则
Therefore,
法二:
-
-
- Taylor:
奇奇怪怪
又神秘的东西
如何定义一个开集
我们称为集合的一个内点开集合:只含有内点的集合称为开集线性空间满足八条原则
什么是数域?
什么是拓扑空间?
设为一个集合为的幂集的子集(所有子集的集合)若:对于任意的都有其中为指标集都有则称为一个拓扑空间势
:可以排序:可数、可列
:不可数、不可列
连续统假设
Reference:《实变函数论》
序结构:分析学
代数结构:代数学
拓扑结构:几何学
区域不变性
数分观点下的不动点
设且则
存在使得即为中的不动点
设在处可微
证明
Solution:
#添项
设试证
存在
Solution:
设在上连续且证明
在上连续
一些常考 Theorem
需要掌握从实数公理推到每一个Th
以及Th之间互推!
- Declekind分割原理
- 确界限存在原理
- 单调有界原理
- 区间套定理
- 有限覆盖定理
- 聚点定理
- 有界数列必有收敛子列
- Cauchy收敛准则