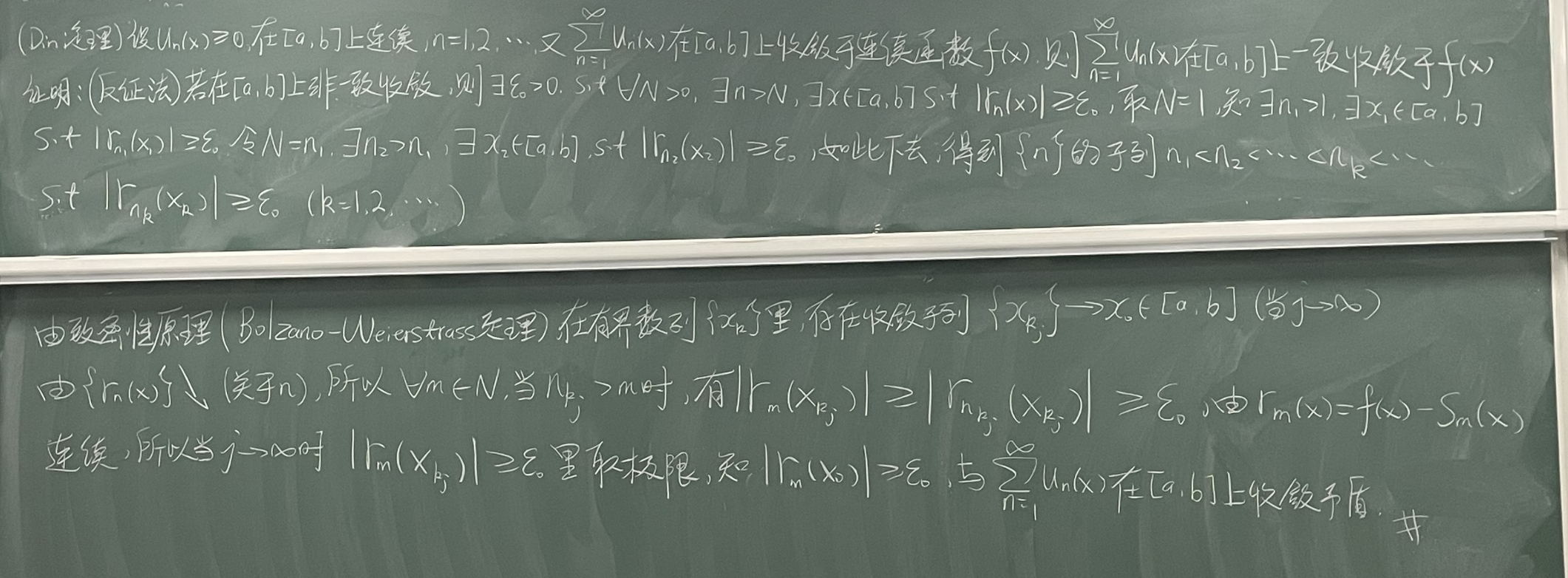2023 Fall Final Exam
积分
可积性及证明
可积的条件(证明见5.2)
可积的必要条件:
- 闭区间可积一定闭区间有界(无界不可积分,可积必有界)
可积的充分条件:
- 闭区间连续必定可积
- 闭区间单调必定可积
- 闭区间有限间断+有界必定可积
其他
- 可积→分段可积
- 可积:证明
Proof
由条件:
有
从而
- 平方可积
- 复合可积
例 证明 Riemann 函数 在 可积
Analysis
设 , 中满足 的有理点 至多有有限个
不妨设有 个,为
对分割 , 记
于是
元素个数
Proof
函数值小于 sigma =>振幅一定小于sigma
的子区间含取分割
Proof.2
摘自陈纪修版本数学分析
由 Riemann 函数的性质, 对任意给定的 ,在 上使得 的点至多只有有限个
不妨设是 个,记为 .
作 的划分 , 使得满足
,
.....
,
,
图 7.1.6 表示的是的情况.由于
而在右边的第一个和式中,有且;
在第二个和式中,有且,
因此得到
.
由定理 7.1.3, Riemann函数可积.
证毕
如图为 (有两个点超出)的情况
满足:1. ;2.
思路:
- 将有限个大于 的点用分割分开,使得分割呈现:包含、不包含交替出现的情况,并且包含的区间满足区间长度小于 从而便于求 Darboux 和时分奇偶分开;
- 包含特定点的区间中
- 含有特定的大点的区间由于 区间长度 小而小(
- 其他的区间由于 振幅小 而小
Darboux 和
设 是分割 添加 个分点的加细分割,则
任意的上和比任意下和大
设 和 是 的任意两分割,则
上、下积分与上、下和
结论:
最小的上界: 特殊上界
可积的第 I 充要条件:上下积分相等
D 函数不可积
设 在 有界,则
设 在 有界,则
分割
要使 :
- 或者 很小
- 或者虽 不小,但其对应的小区间长度和很小
可加性、线性性
略
(闭)子区间可积
※子区间可积
若 , 则对 有
改变有限点不改变可积分性与积分值
※改变有限点不改变可积性与积分值
设 , 除有限点外 . 有
且
- 相当于 修改有限个点得到
- 改变有限点不改变可积性与积分值
- 不可积若可以,则改回去(矛盾)
- 应用: 可知 存在, 由于可补充定义 时
Proof
令 则
除有限点外均为
故 且
又
故 且
⭐估值性:介于函数的最大、最小面积
若 , 且 , 则
⭐积分的绝对值不超过绝对值的积分
若 , 则 , 且
具有启发意义的证明:
Proof
即证:
由于
由 #积分/估值性 三边积分:
以及绝对值可积不能推出函数可积
🔴积分中值定理
设 , 则 使得
Proof
设 在 上最大小值为M, m,则:
由 #积分/估值性
由 #闭区间连续函数介值性 :
使
平均值为:
Proof
见作业
变上限积分
略
连续性:一定连续
可导性:变上限积分求导=被积函数上限处值×上限求导
常与 #LHospital法则 联动使用
原函数存在定理:闭区间连续函数必存在原函数
微积分基本定理:连续函数
设 , 且 , 则
设 且 则
(弱化在: 可积不一定连续)
积分相关计算
例题参见 MA.Add.02.积佬修炼手册,这里只给出一些思路罗列
积分表及补充
积分表
-
;
-
;
常用形式:
-
;
- P.S. 的定义域为 , 的定义域为 故需要绝对值
-
;
-
;
-
;
-
;
-
;
-
;
-
;
P.S.
-
;
-
;
-
.
补充不定积分
- (递推)
不定积分
凑微分法
换元积分法
三角代换 去根号
含无理式
和
时, 可采用
和
等三角代换去根号.
分部积分法
有理函数不定积分
代数学定理 分解
真分式可分解为下列两类简单分式之和
-
;
-
.
实操过程
- 实数范围内分解
- 化为待定形式:
通分
- 分式上下系数相同,解出来
- 带回:
有理式次数较大时, 常用添项法和凑微分法, 通常当分母已因式分解好时才用公式.
三角函数有理式
万能变换适合次数小的三角函数有理式积分
令 , 则
其他
被积函数中含有根式. 常采用第二代换法
去掉根式, 化为有理函数的积分.
原函数非初等的函数
定积分
换元积分法
例 14 设 是周期为 的连续函数. 证明: , 有
周期函数:等于一个周期
在 对 积分
分部积分法
Wallis 公式 EVENPIE
三角函数互换
积分的应用
弧微分公式:ds = √(1+k²)dx
直角坐标方程参数方程
弧长公式:∫ √(1+k²)dx or (x'²+y'²) or (r²+r'²)
弧长公式
设 , 则
设 , 则
若, 则
Proof
例题
例1 求曲线 上点 与 间的弧段长.
Solution
例2 求曲线 弧长.
Solution
例3 求心脏线 全长.
Solution
二倍角注意根号!
例 4 求椭圆 周长.
Solution
遗憾的是, 时属于不可积函数 => 需要查 椭圆积分表(近似)
该类函数被称为椭圆的第二类积分
平面图形面积:∫ f(x) dx = ∫ y(t) dx(t) = 1/2 ∫ r²(θ) dθ
若 的参数方程为 , , 且 , 则曲线 , 与直线 及 轴所围面积
曲线 与射线 及 所围面积
旋转体体积 V = π ∫ f²(x) dx = 2 π ∫ xy dx
曲线 与 及 轴所围图形绕 轴旋转
y轴:
曲线 与 及 轴所围图形绕 轴旋转所得旋转体体积
旋转体侧面积 S = 2π ∫ y √(1+k²) dx
记得可以分成多个等分求!(例如四个象限)
积分余项 Taylor 公式
并不知道会怎么考,见MA.5.1 积分#七、积分余项 Taylor 公式
Lagrange 余项 Taylor 公式
常见级数
来自:【微积分】常用级数与级数审敛法汇总
- 绝对收敛级数(Absolute Convergent Series):级数的每一项都取绝对值后仍然收敛。
- 条件收敛级数(Conditional Convergent Series):因为正负交错而收敛的级数(级数是收敛的交错级数,但是每一项都取绝对值后,就不收敛了)
- 调和级数(Harmonic Series):所有正整数的倒数形成的级数
- P-级数(P-Series):所有正整数的倒数的p幂次形成的级数,又被称为超调和级数。
- 几何级数(Geometric Series):每相邻两项,后项比前项的比值相同,又被称为等比级数。
- 超几何级数:见例题12:
其中
- 时收敛
- 时发散
- 时
- 收敛
- 发散
- 高斯判别法
- 正项级数:每一项都是非负的级数
- 交错级数:正项和负项交替出现的级数
- 幂级数与泰勒级数:见于下面
- 三角级数与傅里叶级数:见下面
- 傅里叶级数:任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示,称为傅里叶级数。
级数的敛散性判断方法
正项级数
- 正项级数收敛判别的基本思想是看 趋向于 0 的速度
- 不存在收敛“最慢”的级数
- 正项级数的判别方法不能用到一般级数的判别方法上。
基本:收敛原理
充要条件:部分和有界
- 裂项:依据交换律即可
- 积分放缩:原函数是一个容易积分的函数,例如:这个例题
比较判别法:大收=>小收,小散=>大散
极限形式 ~ 无穷小/大
设 , 且 , 则
- 当 时, 与 同敛散
- 当 时, 收敛 收敛
- 当 时, 发散 发散
- 理解:极限的比值为,容易联想到: 阶无穷小/大
- :
- :
- :
说明
- 常选择几何级数与 级数作参照级数
- 常估计通项无穷小 对 的阶
Eg. 发散
设 , 且 , 则
- 当 , 且 时, 收敛;
- 当 , 且 时, 发散
- 理解:
- 说明 发散到 ,若此时还能让 不发散到 ,则一定是一个收敛的数列将其拉回来
- 说明 收敛到 ,若此时还能让 不趋近于 ,则一定是一个发散的数列让他拉起来
比值判别法:系数模比值极限 - 小收大散
若正项级数 满足
- , 则 收敛
- , 则 发散
- , 则
- 当 时, 收敛;
- 当 时, 发散;
- 当 时, 判别法失效
简记为:
- 当 时,级数收敛
- 当 时,级数发散
- 当 时,级数可能收敛也可能发散
推论
设 ,且
则
- 收敛 收敛
- 发散 发散
若正项级数 满足
- , 则 收敛
- 有无穷多项使 , 则 发散
- , 则
- 当 时, 收敛;
- 当 时, 发散;
- 当 时, 判别法失效
简记为:
- 当 时,级数收敛
- 当 时,级数发散
- 当 时,级数有可能收敛也有可能发散
Raabe 判别法 (比值法失效时):大收小散
设 , 且
若 , 则 收敛; 若 , 则 发散
- 注意那个奇怪的
- 当级数比几何级数收敛得慢的时候更有效:由于外面乘了一个 ,因此 按照 的量级减小
若交错级数 满足
则 收敛, 且
- 理解: 保证了最后能够越震荡越小,实现收敛
- 保证了第一项是正数(才有后面的范围不等式)
- 若去掉1(非单调)可能震荡
- 条件:通项
- 结论
积分判别法
若非负函数 在 上单减, 则级数

乘积和
🔴 A-D判别法:单调 有界<0=>趋于
设 , 满足下两条件之一: 则 收敛.
(Abel) 单调有界, 收敛;
(Dirichlet) 单调趋于 的部分和有界.
- 要求各有侧重
- 单调有界, 收敛
- 单调趋 , 有界
Eg. 证明 收敛
Proof
凑项倍公差的一半
基本:性质
根据 , 化简+放缩到下标和
Mertens 定理:至少一个绝对收敛
设 且至少其一绝对收敛, 则它们的Cauchy乘积收敛, 且
- 理解:Why绝对收敛?
- 各项趋于零快才能收敛,若条件收敛,各自能够抵消不一定能够实现乘积的抵消
Abel 定理
设 . 若它们的 Cauchy 乘积收敛, 且 , 则
其他
性质
若 , 将其相邻若干项加括号得到的新级数收敛,且和不变
发散 , 但 收敛
设 , 则任意更换顺序求和所得新级数敛散性不变, 收敛时和不变.
收敛的线性性
略
级数 , 均收敛,则 ,, 也收敛
绝对收敛 / 条件收敛
条件Eg. 1-1/2+1/3-1/4+1/5-1/6+...
绝对收敛/条件收敛
若 收敛, 则称 #绝对收敛
若 收敛, 而 发散, 则称 #条件收敛
若 收敛, 则级数 收敛
Proof
由 收敛 Cauchy 准则
绝对收敛的交换律
设 绝对收敛, 则任意改变求和顺序所得新级数也绝对收敛, 且和不变.
Riemann 重排定理
设 条件收敛, 则对 存在改变求和顺序的新级数使之趋于
略
[乘积] Abel 变换 / 分部求和
设有 , 记 , 则
Abel 引理
设 单调, 若 , 则
级数判敛方法总结
来自:Blog by luoyuwen
级数判敛的方法众多,总结起来就有比较判别法,比较判别法的极限形式,比值判别法,根值判别法,极限判别法,积分判别法,交错级数判敛法以及一个级数收敛的必要条件。对于一个具体的级数,应该应用哪一种方法最有效,这就是一个头疼的问题。我们不可能一个方法一个方法的来试,那样就太浪费时间了。这里我们总结一下一般的原则。
判定一个级数是否收敛的关键,在于迅速确定级数的形式。不同的形式有着不同的有效判别方法。现在我们总结一下,哪些形式应用哪些判别法则。
- 如果一眼能看出一般项的极限不趋于 ,即 ,则级数发散;
- 如果级数具有形式 ,那么就是一个 级数。当 时发散,当 时收敛;
- 如果级数具有形式 , 那么就是一个几何级数。当 时发散,当 时收敛;
这两种级数是最基本的级数,后面的几种判别法,差不多都是跟这两种级数做比较而得到的。
- 如果级数的一般项是 的一个代数式(有理分式或者无理分式),那么该级数与某个 级数同敛散(极限判别法或者比较判别法的极限形式)。我们只需要在分式中保留关于 的最高阶项,所得到的项就是这个 级数的一般项。
例如,级数 ,它的一般项 ,所以它与级数 同敛散。在这里,我们将级数的一般项关于 的最高阶项保留,就得到 ,所以级数 就是我们要寻找的那个比较级数 。
再如 ,所以级数 发散;
- 或者,简单地说,就是如果一个级数的一般项等价于一个 级数的一般项,则级数与该 级数同敛散;
- 同上,如果一个级数的一般项等价于一个几何级数的一般项,则级数与该几何级数同敛散;
- 如果级数含有 ,则比值判别法比较有效。 需要注意的是,比值判别法对 级数失效,因而对任何级数一般项 的代数式的级数也失效;
- 如果级数的一般项 , 则首先考虑根值判别法;
- 如果级数的一般项是 的函数 并且==广义积分 较易求得==广义积分 较易求得,则可考虑使用积分判别法。
- 如果级数含有项 ,则是一个交错级数,这时候,必定考虑莱不尼兹判别法(交错级数判别法)。
函数项级数
一致收敛概念辨析
来自:如何理解一致收敛?
约定,形式和:
单点收敛:对某个 收敛, 给定之后相当于数项级数(无变量)
收敛 / 逐点收敛:对于定义域 中每一个 单点收敛,先确定 后确定
一致收敛:对于一个确定的 ,所有在定义域 里的 都会收敛(收敛的程度相似)
一致收敛的几何解释
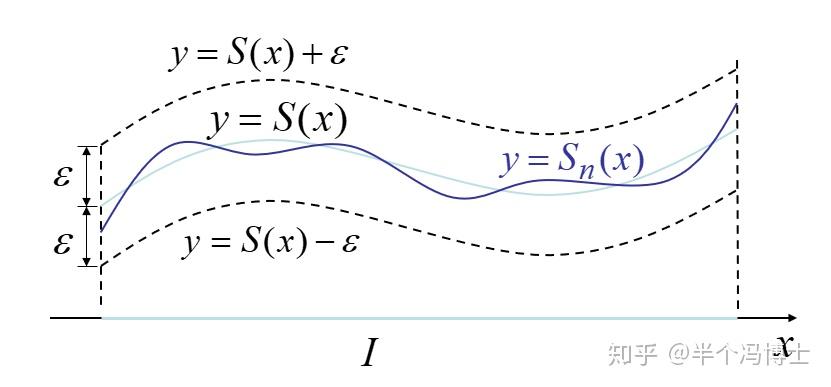
对于划定了一个 的区域,能找到一个 ,对所有 的情形, 无论如何改变,都能在 周围 区域内,即使 的改变会带来一些扰动
因此才有了:
定义: 在 区域内
设 为函数列, 若存在 使
则称 在 上一致收敛于 , 记为
确界极限定理: 越来越大后越来越逼近 (如何衡量?答案是取其中偏差最大的一个,也就是上确界,偏差最大的都趋于 ,则其他的也如此)
一致收敛性的判断
- 利用定义
- 利用 Cauchy 准则
- 利用几个常用的判别法
- Weierstrass 判别法:利用 最大值进行放大,利用不等式,利用 Taylor 公式进行放大
- A-D 判别法
- Dini 定理及其应用
- 利用一致有界
利用定义
设 为函数列, 若存在 使
则称 在 上一致收敛于 , 记为
要用定义证明 在区间 上一致收敛,
先求和函数 , 写出部分和 ,然后对 ,找出与 无关的 ,使得 时有
或者,,即 , s.t.
例题 设函数 在 上有连续的导函数 ,,证明: 在任意有限开区间 内一致收敛于 .
Analysis
即寻找 的关系,故需要构造,注意到, 的表达式具有导数的形式
Proof
由中值定理有:(定义法)
由于 在 上一致连续(连续函数在闭区间上一致连续),
,当 时,有 ,
取 ,则 时,有
此时故当 时, 于 上
放大法
若 s.t. ,且 时 (注意这是充分条件)
例题 在 内一致收敛
Proof
当 充分大时,,故该级数为 #Leibniz级数 ,则在 内一致收敛
补充: #Leibniz级数
绝对值单调递减的交错级数
例如:
设 是一正整数, 证明:
- 方程 在 内有唯一的正实根 ;
- 条件收敛.
确界法 (确界极限定理)
最大的差值(sup)趋于0:当 时,
例题 给定函数列:,试问当 取何值时, 在 上一致收敛
Solution
当 时,,当 时, ,在 处取极大值,
故
由于
因此
当且仅当 时一致收敛
Cauchy 准则判断一致收敛
在 上一致收敛
在区间 上
- 一致收敛 <=> , ,
- 非一致收敛 <=> ,,
例题 讨论级数 的收敛性与一致收敛性
From
Solution
1. 收敛性 由 ,当 时,
由 收敛,故级数在 上一致收敛==(Weierstrass?)==,又因 任意,所以在 内逐点收敛,且内闭一致收敛
2. 一致收敛性 由 ,故 ,当 , 充分大时,有
故当 时
故在 上非一致收敛
利用几个常用判别法
Weierstrass 判别法
利用最大值放大
证明 在 上一致收敛
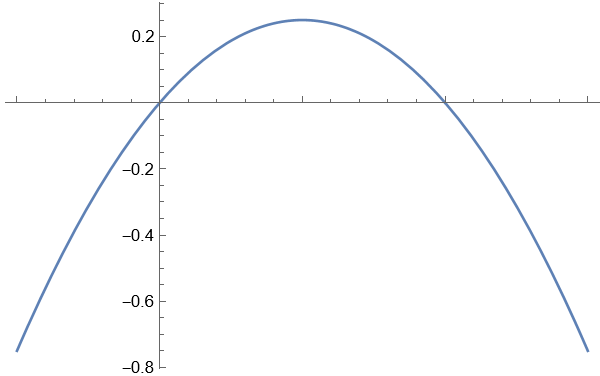
Proof
对通项 求导,令
驻点 ,由
所以 为 上的最大值
收敛
在 上一致收敛
不明意义的插入
在 一致收敛
求通向最大值可得: 的优级数:
利用不等式
证明 在 内一致收敛
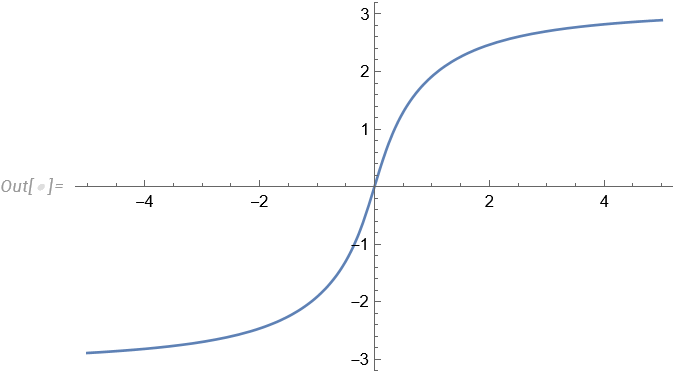
Proof
证明 在任意有限区间 上一致收敛
Proof
利用 Taylor 公式放大
证明 在 内一致收敛
Proof
🔴 A-D 判别法 单调一致 有界 <0=> 趋于
设 满足下列两组条件之一
(Abel)
- 单调, 且在 上一致有界, (关于 )
- 在 上一致收敛;
(Dirichlet)
- 单调, 且在 上一致趋于 0 ,
- 的 在 上一致有界.
在 上一致收敛.
一致有界:
- 单调+一致有界 & 形式和一致收敛
- 单调+一致趋于0 & 形式和一致有界
Abel 判别法与 Dirichlet 判别法联合使用
证明 在 内一致收敛
Analysis
单调一致有界单调一致趋形式和一致有界形式和一致收敛Proof
因为 其中 关于 单调且一致有界:,
由 Abel 判别法,只需要证明 在 内一致收敛
1.
即 在 内一致有界
2.
, ,其关于
又
即
知 一致收敛
Dini 定理:正/负项级数一致收敛于一函数且通项与和一致连续=>收敛于该函数
设函数序列 在闭区间 上点态收敛于 , 如果
- 在 上连续;
- 在 上连续;
- 关于 单调, 即对任意固定的 是单调数列
则 在 上一致收敛于 .
- 理解:连续单调的形式和收敛于连续的函数,则一致收敛
- 注意:不能用开区间
设函数项级数 在闭区间 上点态收敛于 , 如果
- 在 上连续;
- 在 上连续;
- 对任意固定的 是正项级数或负项级数;
则 在 上一致收敛于 .
Proof
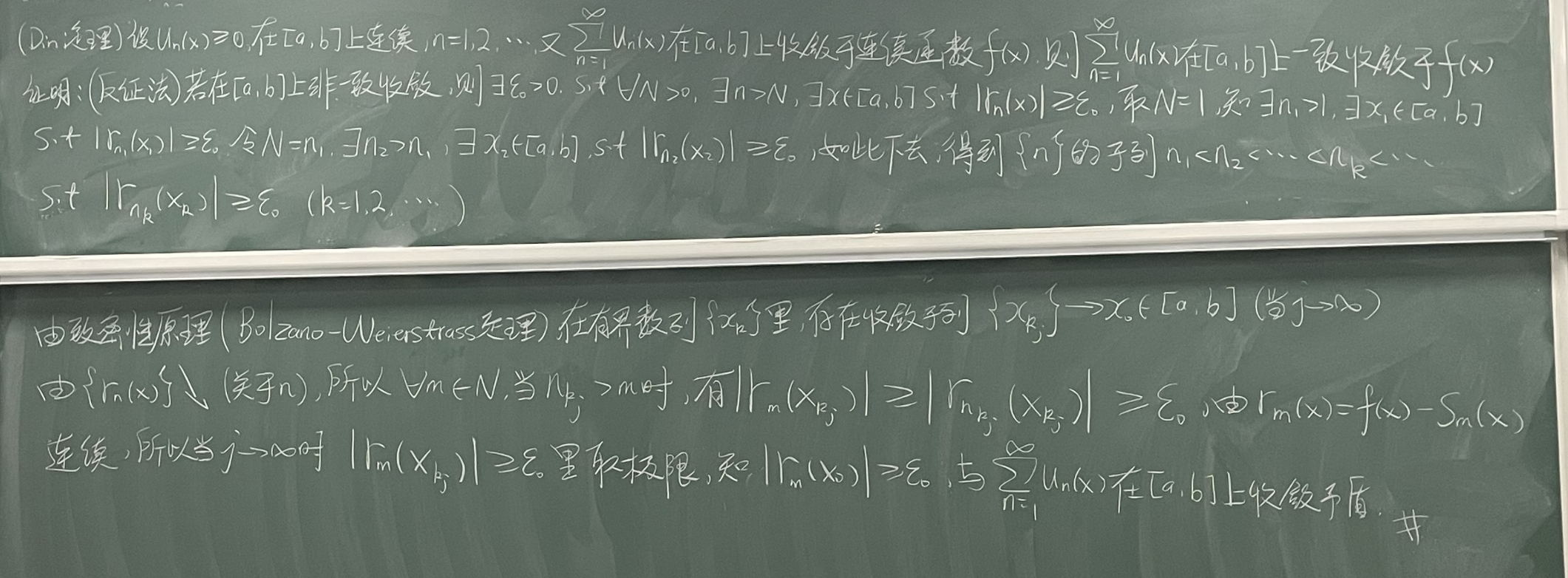
Proof
均在 上连续,故
证明 一致收敛
Proof
对求导 在 上
幂级数
收敛域
Abel 第 I 定理:划定区域
- 若 在 收敛, 则当 时绝对收敛;
- 若 在 发散, 则当 时幂级数发散.
- 理解:收敛区域的大收=>小收,小散=>大散,是包含的关系
- , 无法确定
推论:幂级数收敛情况
幂级数 的收敛仅有三种可能情况:
-
仅在 收敛;
-
在区间 内绝对收敛, 而在 发散;
-
在 (绝对) 收敛.
三种情况可视为以原点为中心的区间, 其长度的一半 称为收敛半径, 称为收敛区间.
收敛半径公式
若 或 , 则幂级数 的收敛半径
- 比值法/根值法求收敛半径(反比)
- 考察端点处收敛性
- 若
- 中心非原点:平移
- 缺项幂级数:变量替换
见 例题
Abel 第 II 定理:幂级数在收敛域中总是内闭一致收敛
设 收敛半径为 , 则它在 内闭一致收敛; 若 时收敛, 则它在 一致收敛
幂级数性质
幂级数的和函数 在收敛区间 内可导, 并有
且求导后的幂级数的收敛半径仍为 .
→ 在收敛域内连续,可逐项求导,可逐项积分
设 ,
则 在 处左连续, 即
幂级数的运算
和函数的求解方法
- 先积分后求导(提出来,让系数和次方一致)
- 先求导后积分
- 拆分成
- 其他
- 两次导数
- 可以合并到 中
- 裂项
- 拆成三个
例3 求下列幂级数的和函数
(1) ;
(2) ;
(3)
Solution
求导:
令
故
又当 时 收敛, 由 Abel. II
故 在 右连续
即:
从而
即
若令
即:
例如
(2) . 令
则 提出来积分
由知
(3)
故
两边积分:
即
由于 ,代入得 ,即
来自竺可桢辅学 - 2022-2023春夏学期数分辅学 级数板块讲义
由 Taylor 公式引入 Taylor 级数,但 级数的收敛性 以及 是否收敛到原函数 需要考虑 收敛半径和余项公式.
常用的初等函数的幂级数展开: (求函数的幂级数展开时: 求导, 积分 , 柯西乘积, 以及在求 类型时可以用 假设法)
- 几何级数的和函数
- 从常见初等函数的幂级数凑微分、凑积分
- 柯西乘积
例题3.1: , 有 , 求 的表达式. (多项式配凑)
例题3.2: 求函数 的幂级数展开式(积分、求导运算类型).
例题3.3: 求 的幂级数展开式. (假设法)
例题3.4: 求级数 的收敛域. (换元)
例题3.5(缺项幂级数): 求 的收敛范围.
例题3.6: 计算无穷级数 的和. (运用基本级数和积分求导运算求幂级数)
例题3.7: 计算积分 . (逐项积分的应用)
例题3.8: (方程式法求和函数) 试求下列幂级数的和函数 .
常用初等函数的幂级数
常用初等函数的幂级数
任意阶绝对值有界,满足- #二项式函数
在 上恒成立
端点情形:
注 特别地, 有
几何级数
例5 将 在 展成幂级数
*当 时。
敛
由此
例6 将 在 展成幂级数
故当时丩站比值失效
故
函数的幂级数展开方法
函数的幂级数展开方法
直接法 先求 , 再利用Taylor公式;
间接法 利用已知的幂级数展开式, 再结合变量
代换、逐项可导、逐项可积性.
例7 将下列函数在 处展成幂级数
-
-
-
例8 设 , 求级数 的和.
根据唯一性
从而
Ex. 设 求
其他知识点